CNN 是什么?
在机器学习中,分类器将类标签分配给数据点。例如,图像分类器为图像中存在的对象产生一个类标签(例如鸟、飞机)。卷积神经网络(CNN)是一种类型的分类器,擅长解决这个问题!
CNN是一种神经网络:用于识别数据中的模式的算法。神经网络通常由一组神经元组成,这些神经元组织成层,每层都有自己可学习的权重和偏差。让我们将CNN分解为多个基本构建模块。
- 一个张量可以被视为一个n维矩阵。在上述CNN中,张量将是三维的,除了输出层。
- 一个神经元可以被视为一个接受多个输入并产生单个输出的函数。神经元的输出在上面被表示为红色→蓝色的激活图。
一个层简单地是具有相同操作的神经元的集合,包括相同的超参数。 - 一个层简单地是具有相同操作的神经元的集合,包括相同的超参数。
- 核权重和偏差,虽然对每个神经元都是独特的,但在训练阶段进行调整,并且允许分类器适应所提供的问题和数据集。它们在可视化中使用黄色→绿色的差异颜色刻度进行编码。具体的值可以通过点击神经元或悬停在卷积弹性解释视图中的核/偏差上来查看交互式公式视图中的。
- CNN表达了一个可微分的评分函数,这在输出层的可视化中表示为类别得分。
如果您之前学习过神经网络,这些术语可能听起来很熟悉。那么CNN有何不同之处呢?CNN利用一种特殊类型的层,恰当地称为卷积层,使它们能够很好地学习图像和类似图像的数据。关于图像数据,CNN可用于许多不同的计算机视觉任务,如图像处理、分类、分割和目标检测。
在CNN Explainer中,您可以看到一个简单的CNN如何用于图像分类。由于网络的简单性,其性能并不完美,但这没关系!CNN Explainer中使用的网络架构Tiny VGG包含了如今最先进的CNN中使用的许多相同层和操作,但规模较小。这样,入门将会更容易理解。
每个网络层都有什么作用?
让我们逐层了解网络中的每一层。在阅读时,可以随意与可视化工具-CNN Explainer进行交互,点击和悬停在不同部分。
输入层(Input Layer)
输入层(最左边的层)代表CNN中的输入图像。因为我们使用RGB图像作为输入,输入层有三个通道,分别对应红色、绿色和蓝色通道,在这个层中显示。当您点击上面的网络详情图标 时,使用颜色标尺显示详细信息(在这一层和其他层上)。
时,使用颜色标尺显示详细信息(在这一层和其他层上)。
卷积层(Convolutional Layers)
卷积层是CNN的基础,因为它们包含了学习到的卷积核(权重),这些卷积核可以提取出区分不同图像的特征,这正是我们进行分类所需要的!当您与卷积层交互时,您会注意到前一层和卷积层之间的联系。每个连接代表一个独特的卷积核,用于卷积操作以生成当前卷积神经元的输出或激活图。
卷积神经元执行一个逐元素的点积运算,使用一个独特的卷积核和前一层对应的神经元的输出。这将产生与独特卷积核数量相同的中间结果。卷积神经元是所有中间结果与学习到的偏置求和的结果。
例如,让我们看一下上面Tiny VGG架构中的第一个卷积层。注意这一层有10个神经元,但前一层只有3个神经元。在Tiny VGG架构中,卷积层是全连接的,意味着每个神经元与前一层的每个神经元都有连接。关注第一个卷积层中最上面的卷积神经元的输出,当我们悬停在激活图上时,我们可以看到有3个独特的卷积核。
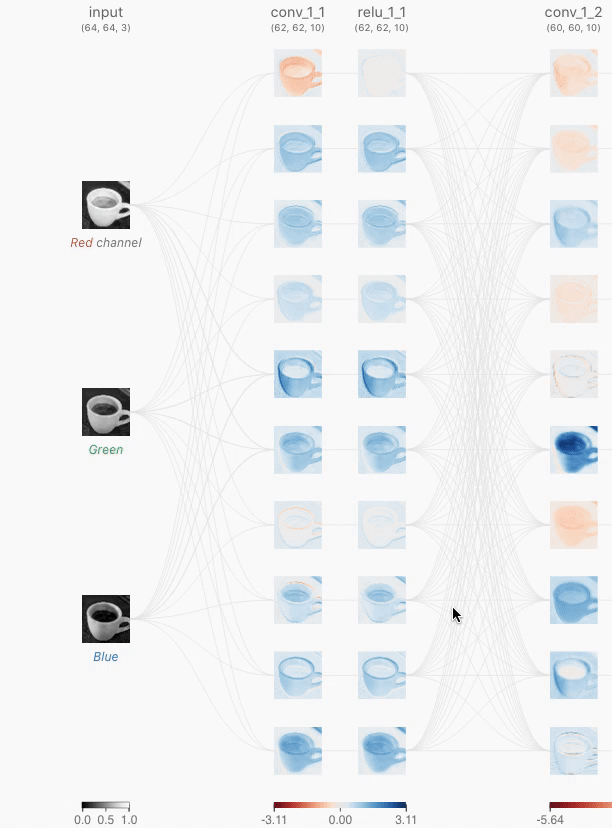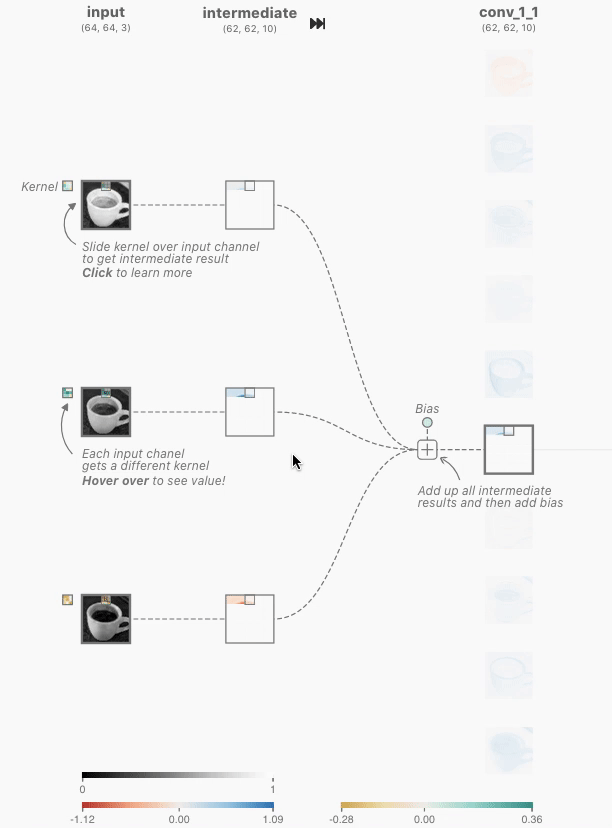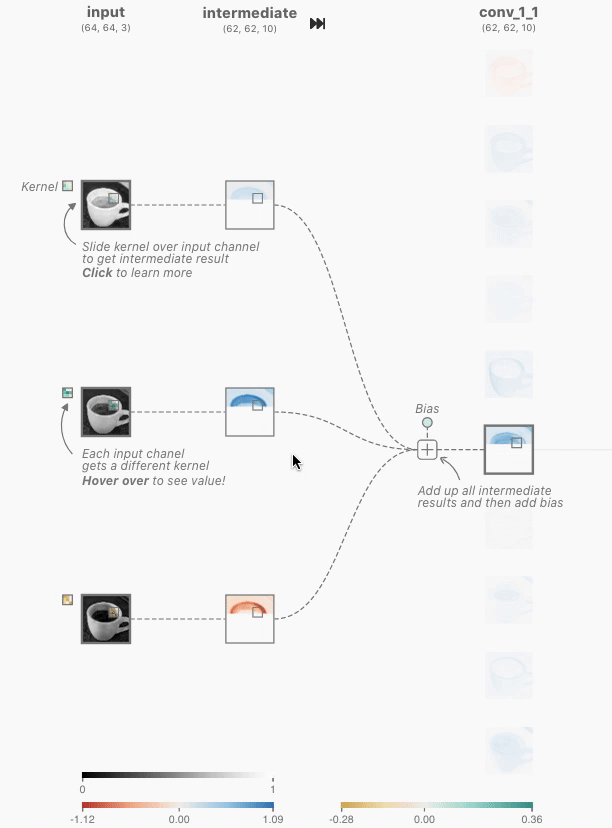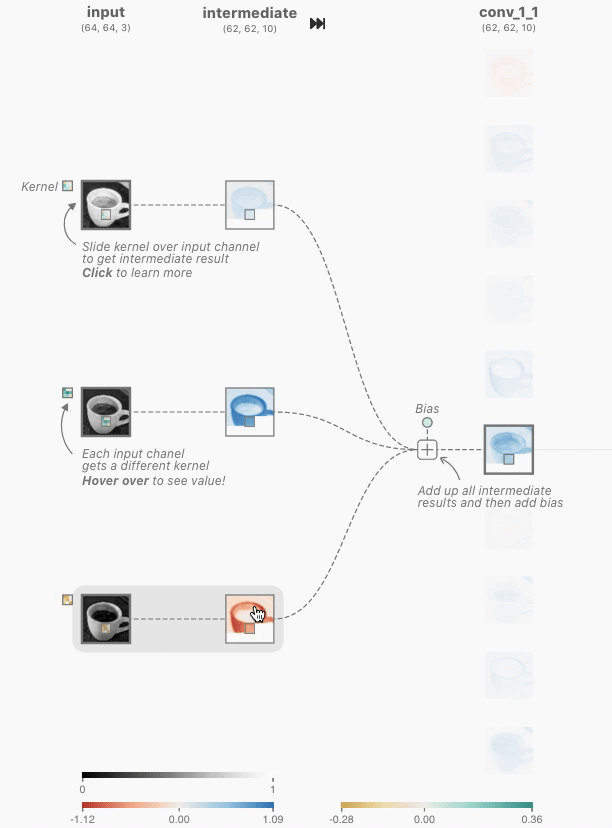
Figure 1. As you hover over the activation map of the topmost node from the first convolutional layer, you can see that 3 kernels were applied to yield this activation map. After clicking this activation map, you can see the convolution operation occuring with each unique kernel.
这些核的大小是由网络架构的设计者指定的超参数。为了产生卷积神经元(激活图)的输出,我们必须对上一层的输出和网络学习的唯一核进行逐元素点积运算。在TinyVGG中,点积运算使用1的步幅,这意味着每个点积中核都会移动1个像素,但这是网络架构设计者可以调整以更好地适应其数据集的超参数。我们必须对所有3个核执行此操作,这将产生3个中间结果。
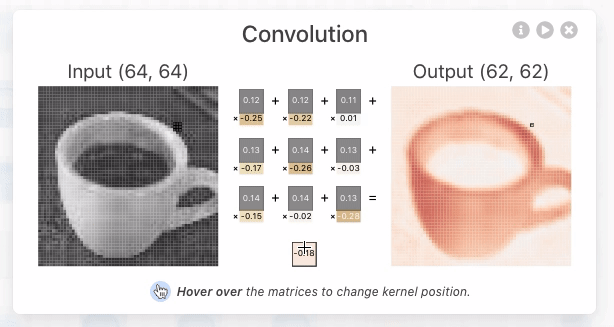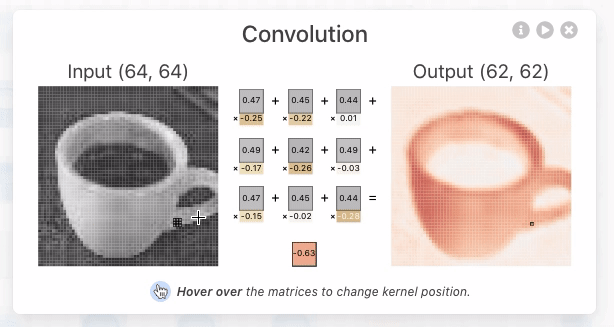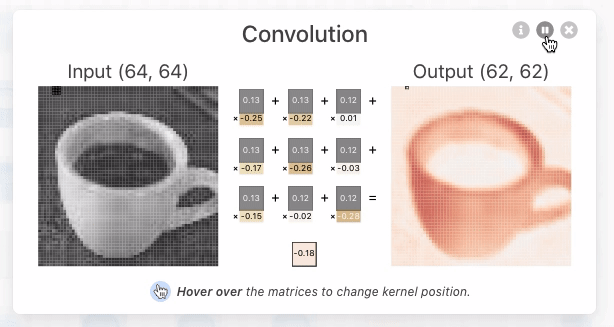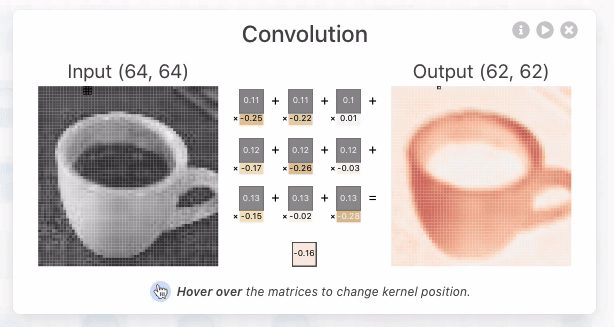
Figure 2. The kernel being applied to yield the topmost intermediate result for the discussed activation map.
然后,执行元素级求和,其中包含所有3个中间结果以及网络学习的偏差。之后,生成的二维张量将是在上述界面中查看的第一个卷积层中最顶层神经元的激活图。必须应用相同的操作来生成每个神经元的激活图。
通过一些简单的数学运算,我们可以推断出在第一个卷积层中有3 x 10 = 30个独特的大小为3x3的卷积核。卷积层与前一层之间的连接是在构建网络架构时的设计决策,这将影响每个卷积层中的卷积核数量。
了解超参数(Hyperparameters)
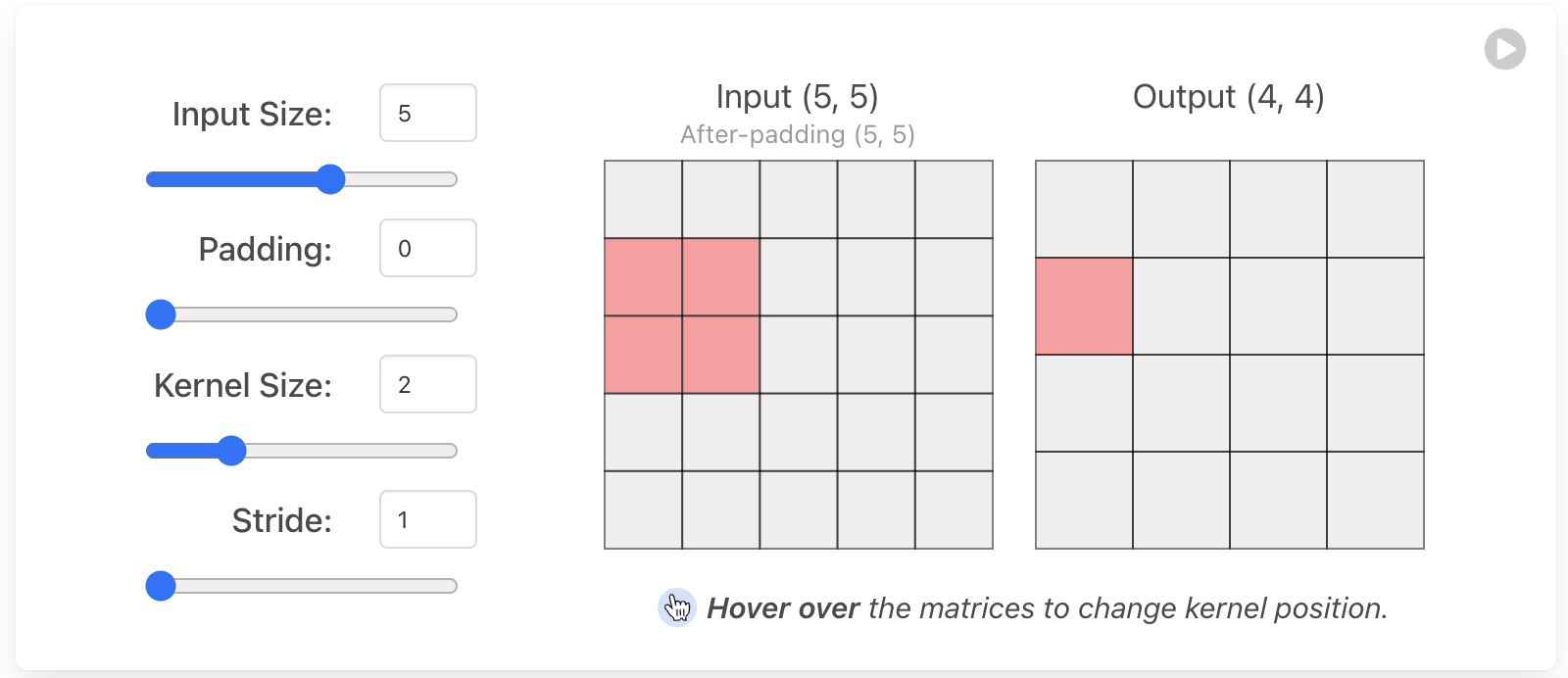
填充(Padding) 通常在卷积核超出激活图时是必要的。填充可以保护激活图边缘的数据,提高性能,并有助于保持输入的空间大小,使架构设计师能够构建更深、性能更高的网络。存在许多填充技术,但最常用的方法是零填充,因为它具有性能好、简单和计算效率高的特点。该技术涉及在输入的边缘对称地添加零。这种方法被许多高性能的CNN(卷积神经网络)如AlexNet所采用。
卷积核大小(Kernel size) ,通常也称为滤波器大小,指的是在输入上滑动窗口的尺寸。选择这个超参数对图像分类任务有巨大影响。例如,小卷积核尺寸能够从输入中提取包含高度局部特征的大量信息。正如您在上面的可视化中所看到的,较小的卷积核尺寸还导致层维度的减小,从而允许更深的架构。相反,大卷积核尺寸提取较少信息,导致层维度更快地减小,通常导致性能更差。大卷积核更适合提取较大的特征。最终,选择适当的卷积核大小将取决于您的任务和数据集,但一般来说,较小的卷积核大小能够提高图像分类任务的性能,因为架构设计者能够将更多层叠加在一起,以学习更复杂的特征!
步幅(Stride) 表示卷积核每次应移动多少像素。例如,如上所述的卷积层示例中,Tiny VGG在其卷积层中使用步幅1,这意味着对输入的3x3窗口执行点积以产生输出值,然后每次后续操作都向右移动一个像素。步幅对CNN的影响类似于卷积核大小。随着步幅减小,学到的特征更多,因为提取更多数据,这也导致更大的输出层。相反,随着步幅增加,这导致特征提取受限,并且输出层尺寸更小。架构设计者的责任之一是确保在实现CNN时卷积核对输入进行对称滑动。使用上面的超参数可视化来改变各种输入/卷积核维度上的步幅,以理解这个约束!
激活函数(Activation Functions)
ReLU
神经网络在现代技术中非常普遍——因为它们非常准确!如今性能最高的CNN由大量层组成,能够学习更多特征。这些开创性的CNN能够实现如此巨大的准确性,部分原因是它们的非线性特性。ReLU将非线性引入模型中,这是非常必要的。非线性对于产生非线性决策边界是必要的,这样输出就不能被写成输入的线性组合。如果没有非线性激活函数,深度CNN架构将退化为一个等效的卷积层,性能远不如现在。ReLU激活函数被专门用作非线性激活函数,而不是其他非线性函数,比如Sigmoid,因为经验观察表明使用ReLU的CNN训练速度更快。
ReLU 激活函数是一种one-to-one的数学运算: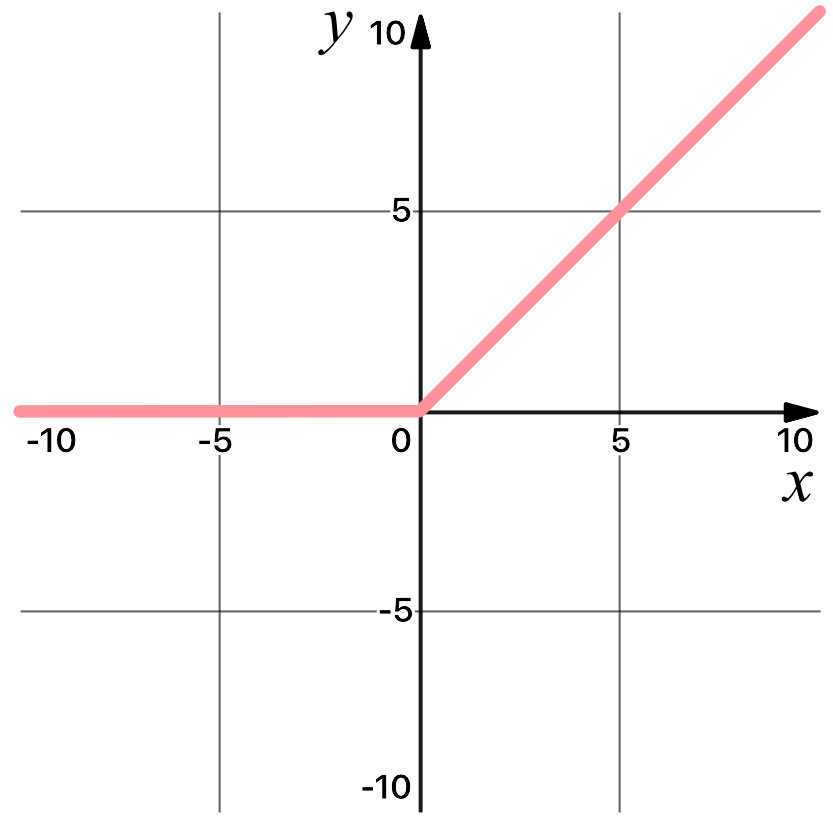
Figure 3. The ReLU activation function graphed, which disregards all negative data.
该激活函数是对输入张量中的每个值逐元素应用的。例如,如果在值2.24上应用ReLU,则结果将是2.24,因为2.24大于0。您可以通过点击上面网络中的ReLU神经元来观察此激活函数的应用。在上述网络架构中的每个卷积层之后执行修正线性激活函数(ReLU)。注意此层对网络中各个神经元的激活图的影响!
Softmax
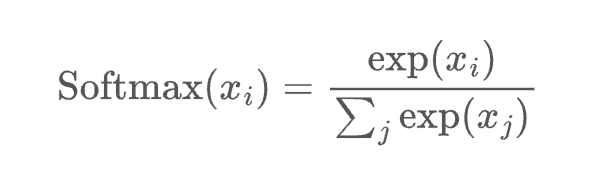
一个softmax操作起到了关键作用:确保CNN的输出总和为1。因此,softmax操作对于将模型输出缩放为概率非常有用。单击最后一层可以看到网络中的softmax操作。注意,展开后的logits没有在0到1之间进行缩放。为了直观地显示每个logit(未缩放的标量值)的影响,它们使用浅橙色到深橙色的颜色比例进行编码。经过softmax函数处理后,每个类现在对应适当的概率!
也许你会想到标准归一化和softmax之间的区别——毕竟,它们都将logits重新缩放到0到1之间。请记住,反向传播是训练神经网络的关键方面——我们希望正确答案具有最大的“信号”。通过使用softmax,我们实际上是在“近似”argmax,同时获得了可微性。重新缩放不会使最大值比其他logits显著地更高,而softmax会。简而言之,softmax是一个“更柔和”的argmax。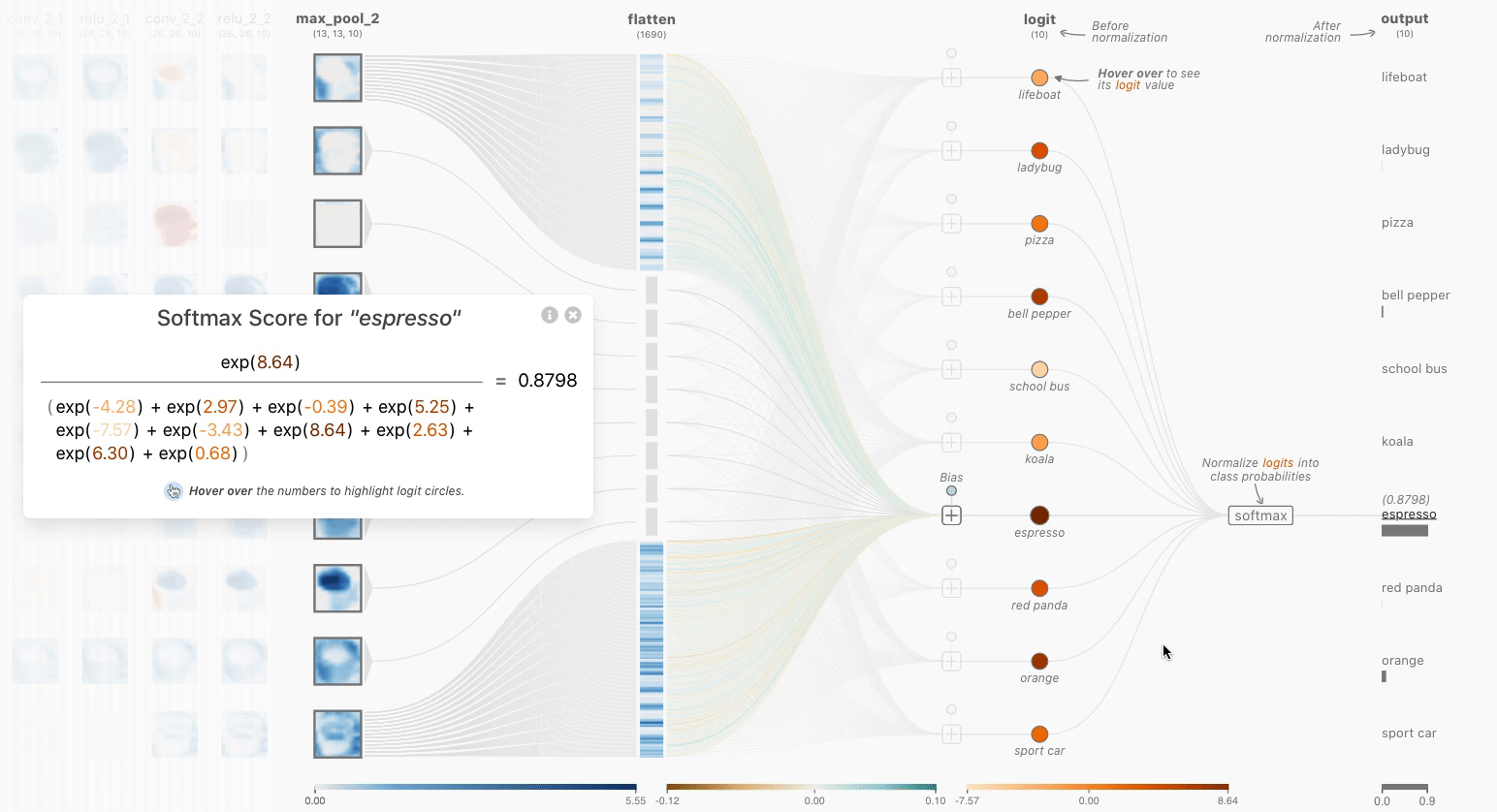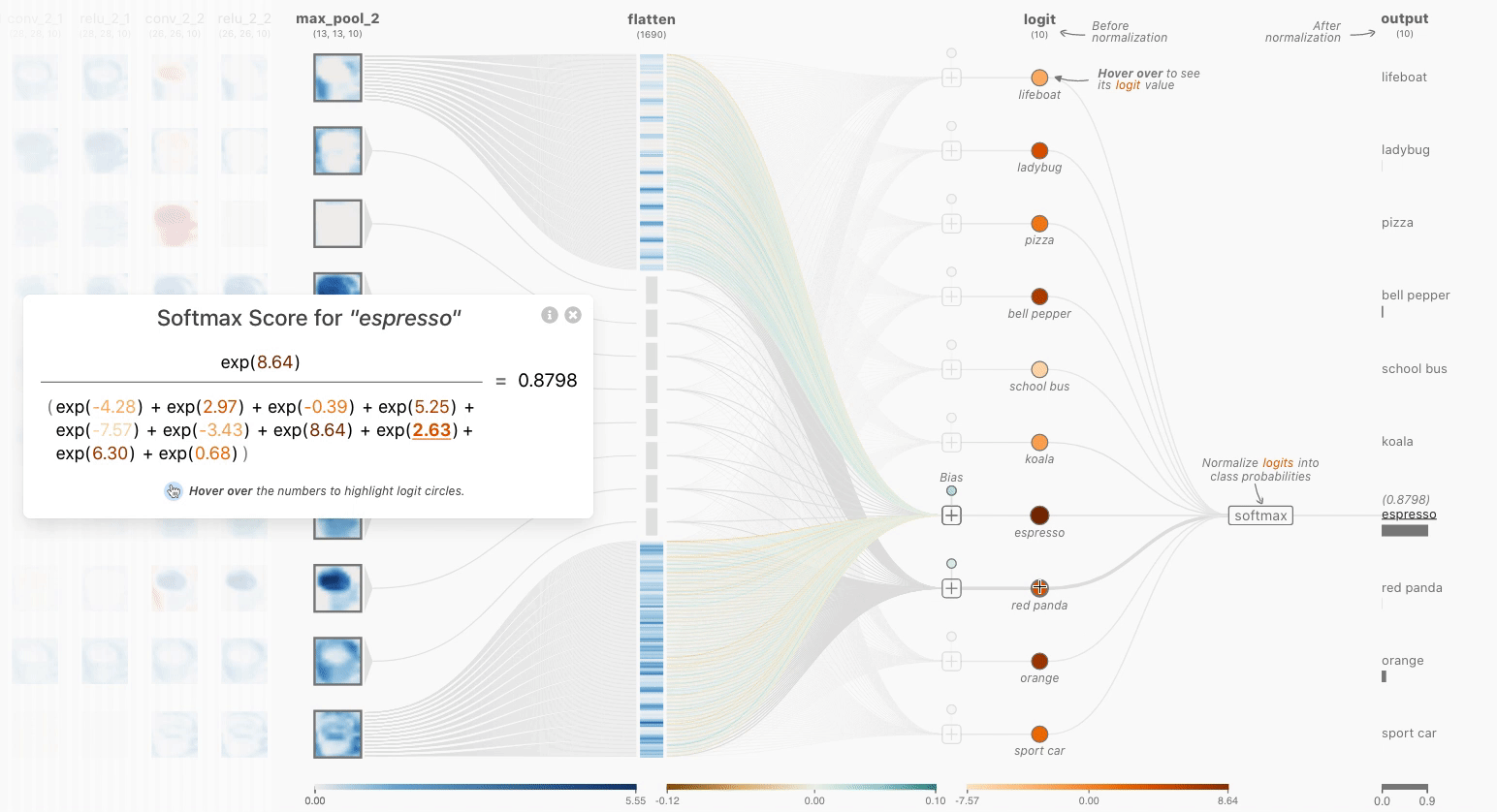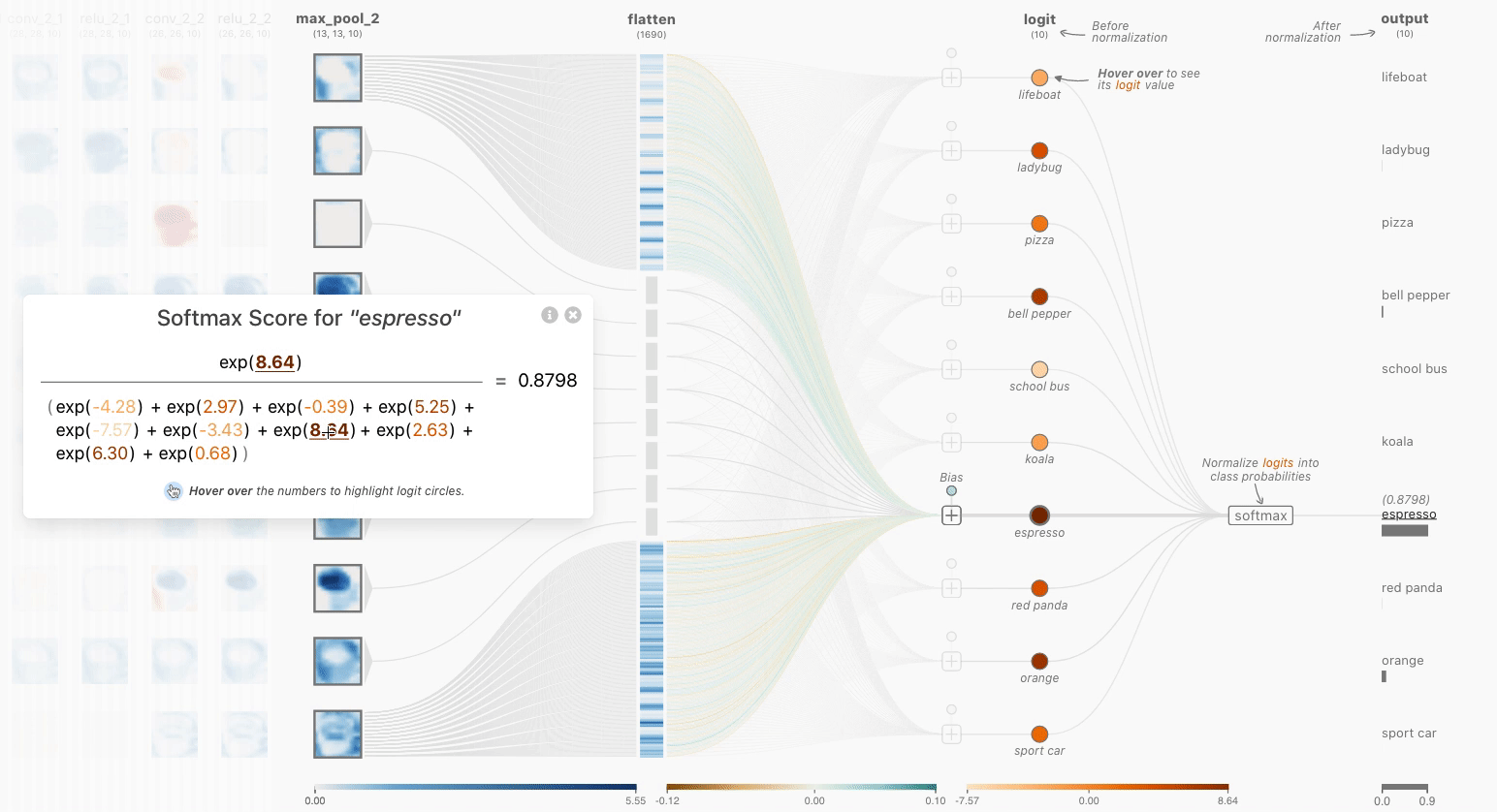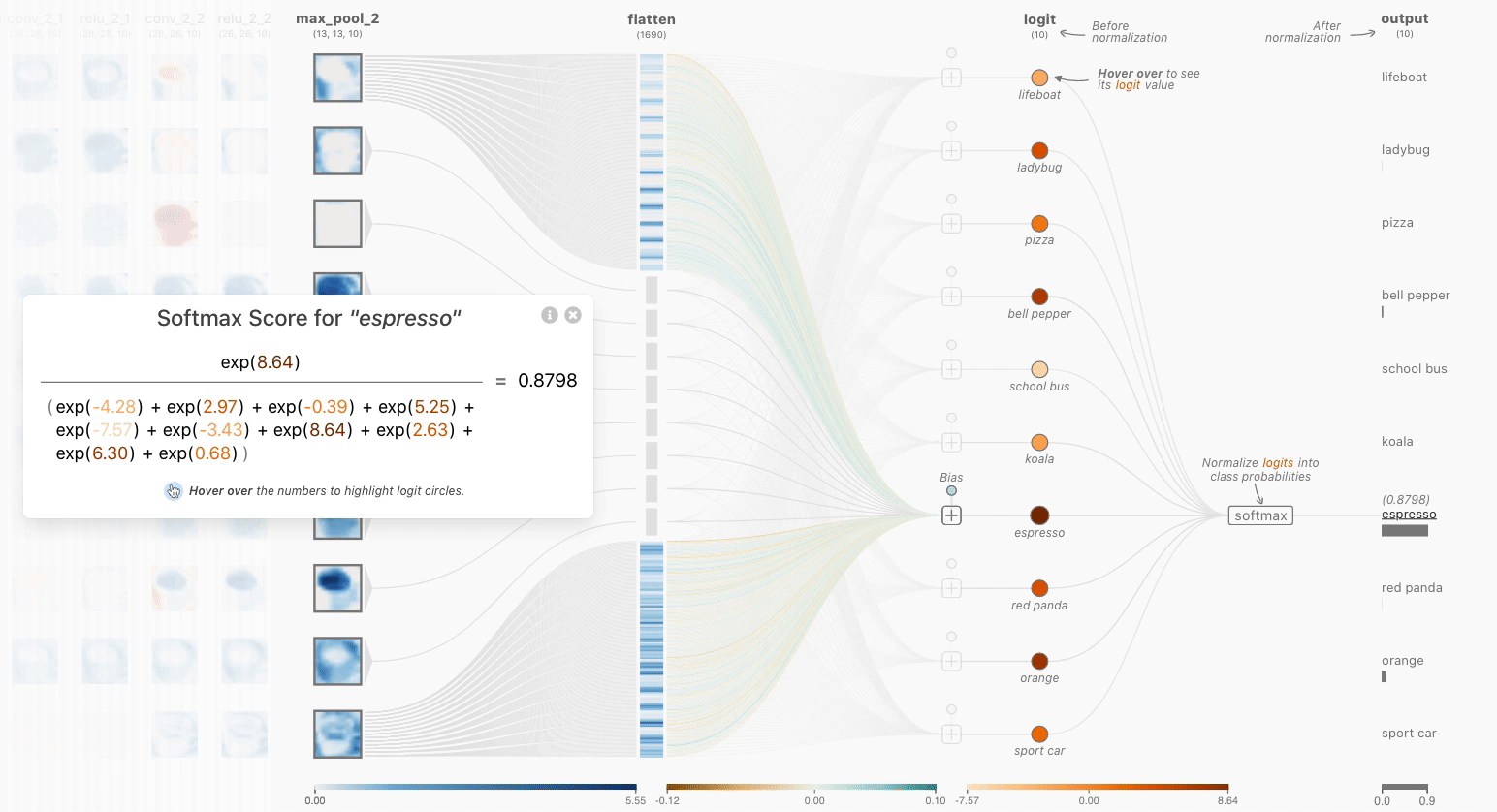
Figure 4. The Softmax Interactive Formula View allows a user to interact with both the color encoded logits and formula to understand how the prediction scores after the flatten layer are normalized to yield classification scores.
池化层(Pooling Layers)
不同的CNN架构中有许多种类型的池化层,但它们都旨在逐渐减少网络的空间范围,从而减少网络的参数和整体计算。上面的Tiny VGG架构中使用的池化类型是最大池化。
最大池化操作在架构设计过程中需要选择核大小和步幅长度。一旦选择了,该操作会在输入上滑动指定步幅的核,而仅选择每个核切片中的最大值,以产生输出的值。可以通过点击上面网络中的池化神经元来查看该过程。
在上述的Tiny VGG架构中,池化层使用2x2的核和步幅为2。这种具体规格的操作导致了75%的激活被丢弃。通过丢弃这么多数值,Tiny VGG更具计算效率,并避免过拟合。
展平层(Flatten Layer)
该层将网络中的三维层转换为一维向量,以适应用于分类的全连接层的输入。例如,一个5x5x2张量将被转换为大小为50的向量。网络的先前卷积层从输入图像中提取特征,但现在是对这些特征进行分类的时候了。我们使用softmax函数对这些特征进行分类,这需要一个一维输入。这就是为什么需要展平层。可以通过单击任何输出类来查看这一层。
资料来源
- https://poloclub.github.io/cnn-explainer/
- 视频教学